Funciones expotenciales
Formula general
La forma general para una función exponencial es y = b·ax donde estánconstantes a y b. b se puede considerar el valor inicial. Esto es porque, cuando x = 0, ax = 1, tan b·ax= b. El valor de a determina el índice de crecimiento o el decaimiento.
Funciones exponenciales donde a > 1 es funciones de crecimiento exponencial. Esto es porque el valor de la función aumenta siempre. Funciones exponenciales donde a < 1 se llama las funciones del decaimiento exponencial porque el valor de la función disminuye siempre
Modelo grafico
Dibuje la gráfica de F(x)=2x+1 .
 Solución:
Solución:Dominio: (-∞,∞)Alcance: (1,∞)Como a=2>1 por lo tanto la gráfica de la función es creciente en todo su dominio.
Pasa por el punto (0,2), que es el intercepto en el eje de y, no hay intersecciones en el eje de x.limx→-∞(2x+1)=1 → y=1 es una asíntota horizontal por la izquierda
Funcion logaritmica y modelo grafico
La función logarítmica "básica" es la función,y = log b x , donde b > 0 y b ≠ 1.
La gráfica de la función logarítmica y = log 10x se muestra a continuación.

Observe que la función logarítmica es la inversa de la función exponencial y = b x y tiene las siguientes propiedades.
- El dominio es el conjunto de todos los números reales positivos.
- El rango es el conjunto de todos los números reales.
(Ya que la función logarítmica es la inversa de la función exponencial, el dominio de la función logarítmica es el rango de la función exponencial y el rango de la función logarítmica es el dominio de la función exponencial) - La función es continua y uno-a-uno.
- El eje de las y es la asíntota de la gráfica.
- La gráfica intersecta al eje de las x en (1, 0). Esto es, la intercepción en x es 1.
Propiedades de los logaritmos
. El logaritmo de un producto es igual a la suma de los logaritmos de los factores:

Ejemplo

2. El logaritmo de un cociente es igual al logaritmo del dividendo menos el logaritmo del divisor:

Ejemplo

3. El logaritmo de una potencia es igual al producto del exponente por el logaritmo de la base:

Ejemplo

4.El logaritmo de una raíz es igual al cociente entre el logaritmo del radicando y el índice de la raíz:

Ejemplo

5. Cambio de base:

Ejemplo

Cambio de base
cambio de base logoritmo se utiliza para cambiar la base de logaritmos. El cambio de la fórmula baja es 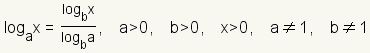 .
.
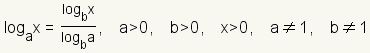 .
.
Cuando los logaritmos primero fueron inventados, no había calculadoras. Los matemáticos y los astrónomos utilizaron los libros publicados con las tablas de logaritmos. Cada tabla tenía exactamente una base. Para encontrar un logaritmo con otra base, utilizaron el cambio de la fórmula baja.
Hoy, la mayoría de las calculadoras y de los programas de computadora basados matemáticas tienen logaritmos en dos bases: base 10 y base e. Para encontrar un logaritmo en cualquier otra base, una debe utilizar el cambio de la fórmula baja.
Ecuaciones expotenciales y logarutmicas
En algunas ecuaciones exponenciales es necesaria la aplicación de logaritmos para poder resolverlas. Esto ocurre básicamente cuando las exponenciales no tienen la misma base. Por ejemplo, la solución de la ecuación es
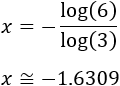 En esta página vamos a resolver 10 ecuaciones de este tipo. Para comprender los pasos se necesita conocer la definición y las propiedades de los logaritmos que damos a continuación.
En esta página vamos a resolver 10 ecuaciones de este tipo. Para comprender los pasos se necesita conocer la definición y las propiedades de los logaritmos que damos a continuación.
Nota: no calcularemos las soluciones complejas.
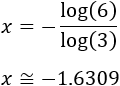
Nota: no calcularemos las soluciones complejas.
2. Definición y propiedades del logaritmo
El logaritmo en base del número positivo se denota por y su valor es el número al que se debe elevar la base del logaritmo, , para obtener el número . Es decir,
Las propiedades de los logaritmos son las siguientes:
*La tercera propiedad es principalmente la que facilita la resolución de las ecuaciones exponenciales puesto que permite escribir la incógnita (que está en el exponente) como un factor que multiplica a un número (al logaritmo).
Ejmplos:
- el logaritmo en base 2 de 8 es 3 porque 2 al cubo es 8:
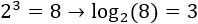
- el logaritmo en base 10 de 100 es 2 ya que 10 al cuadrado es 100:
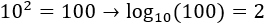
- el logaritmo en base (logaritmo natural, ) de es 3 ya que al cubo es :
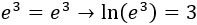
Logaritmo del producto:
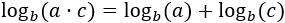 |
Logaritmo del cociente:
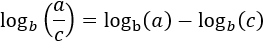 |
*Logaritmo de la potencia:
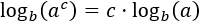 |
Cambio de base:
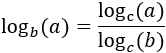 |
Propiedad útil en la práctica:
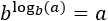 |
Funciones trigonométricas
son las funciones establecidas con el fin de extender la definición de las razones trigonométricas a todos los números reales y complejos.
Las funciones trigonométricas son de gran importancia en fisica, astronomía, cartografía, náutica, telecomunicaciones, la representación de fenómenos periódicos, y otras de muchas aplicaciones.

Las funciones y = sin x, y = cos x, y = tg x.
Conviene que comencemos repasando la noción trigonométrica de seno, coseno y tangente de un ángulo.
Sea un triangulo rectángulo, como el del gráfico presente, siendo los catetos los lados "a" y "b", y la hipotenusa el lado mayor (opuesto al ángulo recto) "c". Las relaciones entre los catetos y la hipotenusa se llaman seno, coseno y tangente, es decir:
El seno (sin ó sen) es el cociente entre el cateto opuesto al ángulo y la hipotenusa.
El coseno (cos) es el cociente entre el cateto adjunto al ángulo y la hipotenusa.
La tangente (tg ó tan) es el cociente entre el cateto opuesto al ángulo y la hipotenusa.
La tangente puede considerarse también como el cociente del seno entre coseno.
El coseno (cos) es el cociente entre el cateto adjunto al ángulo y la hipotenusa.
La tangente (tg ó tan) es el cociente entre el cateto opuesto al ángulo y la hipotenusa.
La tangente puede considerarse también como el cociente del seno entre coseno.
- En Cálculo los ángulos suelen expresarse en radianes más bien que en grados. Siga el enlace si no domina bien el concepto de "radian".
- Como c > a y también c > b, se tiene que el seno y el coseno no pueden supera al valor 1; cosa que no sucede con la tangente. Por otra parte, lo valores de a y b pueden ser positivos o negativos:
Características
Las características fundamentales de la función seno son las siguientes:
Su dominio es R y es continua.
Su recorrido es [- 1, 1] ya que - 1 ≤ sen x ≤ 1 .
Corta al eje X en los puntos k·π con k∈Z .
Corta al eje Y en el punto (0, 0) .
Es impar, es decir, simétrica respecto al origen.
sen (- x) = - sen (x)
Es estrictamente creciente en los intervalos de la forma (a, b) donde a = - π/2 + 2·k·π y b = π/2 + 2·k·π siendo k∈Z .
Es estrictamente decreciente en los intervalos de la forma (a, b) donde a = π/2 + 2·k·π y b = 3π/2 + 2·k·π siendo k∈Z .
Tiene infinitos máximos relativos en los puntos de la forma (π/2 + 2·k·π, 1) con k∈Z .
Tiene infinitos mínimos relativos en los puntos de la forma (3π/2 + 2·k·π, - 1) con k∈Z .
Es periódica de periodo 2π .
sen (x) = sen (x + 2π)
La función f(x) = sen (k·x) es periódica de periodo p = 2π/k
Para |k|>1 el periodo disminuye y para 0 < |k| <1 el periodo aumenta.
-Está acotada superiormente por 1 e inferiormente por - 1.
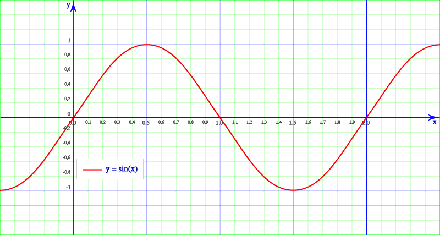
Modelo gráfico
https://youtu.be/uMPx37LRI2E
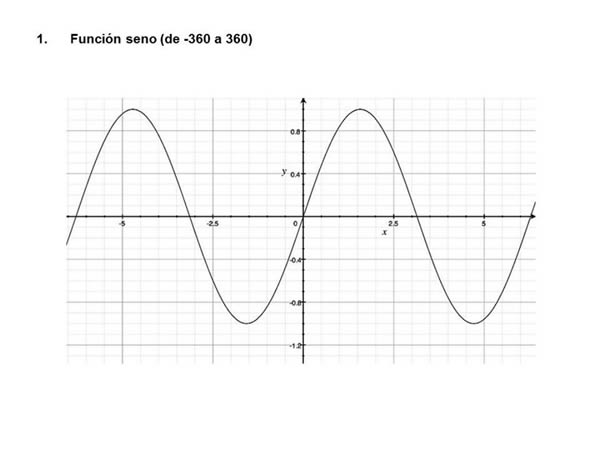
No hay comentarios:
Publicar un comentario