Función Racional

Una función racional de una variable es una función que puede ser expresada de la forma:

${\displaystyle f(x)={\frac {P(x)}{Q(x)}}}$

donde P y Q son polinomios y x una variable, siendo Q distinto del polinomio nulo, esta fracción es irreducible, es decir que las ecuaciones P(x) = 0 y Q(x) = 0 carecen de raíces comunes. Esta definición puede extenderse a un número finito pero arbitrario de variables, usando polinomios de varias variables.

La palabra "racional" hace referencia a que la función racional es una razón o cociente (de dos polinomios); los coeficientes de los polinomios pueden ser números racionales o no.

Las funciones racionales tienen diversas aplicaciones en el campo del análisis numérico para interpolar o aproximar los resultados de otras funciones más complejas, ya que son computacionalmente simples de calcular como los polinomios, pero permiten expresar una mayor variedad de comportamientos.

Ejemplo: 

https://www.youtube.com/watch?v=nnAphQdFmJ0 

funciones cuadraticas

se denomina función al vínculo entre dos conjuntos a través del cual a cada elemento del primer conjunto se le asigna un solo elemento del segundo conjunto o ninguno. La idea de cuadrático, por otra parte, también se usa en el ámbito de las matemáticas, aludiendo a aquello relacionado con el cuadrado
función cuadrática a la función matemática que se puede expresar como una ecuación que tiene la siguiente forma: f (x) = ax al cuadrado + bx + c.
a, b y c son los términos de la ecuación: números reales  con a siempre con valor diferente a 0.

Caso 1 La parábola intercepta el eje de las x− en dos puntos.

Un ejemplo de este caso es 

y=x2+x−6.

Podemos encontrar las soluciones a la ecuación x2+x−6=0haciendo y=0. Resolvemos la ecuación factorando: (x+3)(x−2)=0, así x=−3 o x=2.

Otra forma de encontrar las soluciones es graficar la función y obtener los intersectos en x− a partir de la misma. Vemos que la parábola intercepta el eje de las x− en x=−3 y x=2.

Cuando la gráfica de una función cuadrática intercepta el eje x en dos puntos, obtenemos dos soluciones distintas para la ecuación cuadrática.

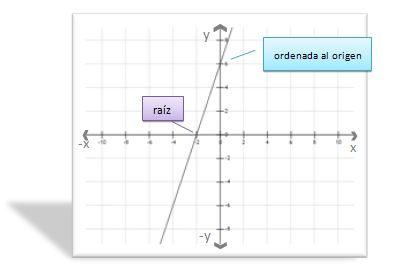
raíces  y el discriminante 

Raíces de una Función Cuadrática

La siguiente aplicación nos muestra otra forma de expresar las funciones cuadráticas.

En la aplicación anterior al escoger a = 1, $r$ 1 = 1 y $r$ 2 = 2 resulta la gráfica de la ecuación cuadrática
Selecciona la caja rotulada Intersección con el eje. Nota que $r$ 1 y $r$ 2 son los valores de x donde f(x) = 0. Estos valores se conocen como las raíces de la función cuadrática.
Si realizamos la multiplicación, obtenemos la fórmula de la función correspondiente en su forma general.

Esto nos indica que si tenemos la fórmula y la factorizamos obtenemos las raíces de una función cuadrática. En esta sección utilizaremos lo aprendido en la lección de factorización.

https://www.youtube.com/watch?v=klfx35lUALU

formas estandar 

La forma estándar de una ecuación cuadrática es y = ax^2 + bx + c, donde a, b y c son coeficientes y la y y la x son variables. Es más fácil resolver una ecuación cuadrática cuando está en su forma estándar ya que puedes computar la solución con a, b y c. De todos modos, si necesitas graficar la función cuadrática, o parábola, el proceso es más simple cuando la ecuación está en la forma canónica. Esta es de la forma: y = m(x-h)^2 + k

Encuentre el vértice de la gráfica de cada función y lo identifican como un punto mínimo o máximo. 
a) f (x) = - (x + 2) ² - 1 
b) f (x) =-x ² + 2 
c) f (x) = 2 (x - 3) ²

a) f (x) = - (x + 2)² - 1 = - (x - (-2)) ² - 1 
a = -1, h = -2, k = -1. El vértice está en (-2, -1) y es un punto máximo ya que es negativo. 

b) f (x) =-x ² + ² = - (x - 0) ² + 2 
a = -1, h = 0 y k = 2. El vértice está en (0,2) y es un punto máximo ya que es negativo. 

c) f (x) = 2 (x - 3) ² = 2 (x - 3) ² + 0 
a = 2, h = 3 y k = 0. El vértice está en (3,0) y es un punto mínimo desde que es positivo.

https://www.youtube.com/watch?v=tnIUrm-sgho

 Forma factorizada

    Toda función cuadrática se puede factorizar en función de sus raíces. Dada:

    se puede factorizar como:

    siendo a el coeficiente principal de la función, por ello se extrae siempre como factor común, de no escribirse, el coeficiente de x² sería siempre 1. x₁ y x₂ representan las raíces de f(x). En el caso de que el Discriminante Δ sea igual a 0 entonces x₁ = x₂ por lo que podríamos escribir:

    En este caso a x₁ se la denomina raíz doble, ya que su orden de multiplicidad es 2.

https://www.youtube.com/watch?v=QpuVMeFUppQ

Matematicas

FUNCIONES LINEALES

Modelo grafico:Cada una de las ecuaciones que forman un sistema lineal de dos ecuaciones con dos incógnitas es la de una función de primer grado, es decir, una recta. El método gráficopara resolver este tipo de sistemas consiste, por tanto, en representar en unos ejes cartesianos, o sistema de coordenadas, ambas rectas y comprobar si se cortan y, si es así, dónde. Esta última afirmación contiene la filosofía del proceso de discusión de un sistema por el método gráfico. Hay que tener en cuenta, que, en el plano, dos rectas sólo pueden tener tres posiciones relativas (entre sí): se cortan en un punto, son paralelas o son coincidentes (la misma recta). Si las dos rectas se cortan en un punto, las coordenadas de éste son el par (x, y) que conforman la única solución del sistema, ya que son los únicos valores de ambas incógnitas que satisfacen las dos ecuaciones del sistema, por lo tanto, el mismo es compatible determinado.

Ejemplo:Sistema 1

Resolver gráficamente el siguiente sistema de ecuaciones:

Ver solución

Lo primero que hacemos es despejar la $y$ en ambas ecuaciones.

Primera ecuación:

Segunda ecuación:

Ahora vamos a calcular unos cuantos puntos de las dos funciones para representarlas. Utilizaremos $x=0$ y $x=2$.

Para la primera función tenemos la tabla

Para la segunda función tenemos la tabla

Para la segunda función tenemos la tabla

Ahora representamos los puntos de cada tabla uniéndolos:

La solución del sistema es el punto donde las gráficas se cortan

Ejercisio:

Sistema 2
Resolver gráficamente el siguiente sistema de ecuaciones:

Modelo algebraico:

Los modelos algebraicos son una herramienta que nos ayuda a solucionar problemas cotidianos, cuando no contamos con dos datos o más. Para construir este tipo de modelos, debemos traducir el lenguaje cotidiano al lenguaje algebraico, para lo cual representamos las incógnitas con una literal; formamos una expresión, y hacemos uso de la igualdad  “ =  “ para así establecer la ecuación a resolver.

En todo momento el modelo proporciona la fórmula del problema. Es una representación simplificada del mundo verdadero, incluye variables pertinentes que se pueden controlar. Por ejemplo, un modelo de caída libre de los cuerpos no se refiere a variables como color, textura, o la forma del cuerpo involucrado. Es así como un modelo no puede incluir todas las variables porque por medio de un número pequeño de variables pueden explicar la mayoría de los fenómenos.

La mayoría de los modelos son simbólicos porque los símbolos representan las propiedades del campo de estudio que se desee. Los primeros modelos eran de representaciones físicas tal como modelos para el comportamiento de aviones, tanques de remolque, barcos, porque los modelos físicos son en comparación con otros fáciles de construir.

Ejemplo:

En el problema planteado, la incógnita es el número que le tenemos que sumar a 10 y restar a 18 para obtener la misma cantidad.

Posteriormente, es necesario representar la incógnita con una letra o literal x.

Al sustituir el valor que deseamos encontrar por la literal “x”, en el ejemplo que estamos analizando, formaríamos la expresión 10 + x, así como 18 - x. Si decimos que los resultados de estas expresiones deben ser iguales entonces podemos representarlas con la siguiente expresión:

10 + x = 18 - x

Encontrar el número buscado, se reduce entonces, a encontrar un número tal, que al ser sustituido por la literal x, en la expresión anterior, haga que en ambos lados se obtenga el mismo valor.

No ha sido una casualidad que usemos la palabra expresión para referirnos a 10 + x, 18 - x, así como a 10 + x = 18 - x.  El concepto expresión está relacionado al lenguaje o lengua.  Es muy común usar como sinónimos expresión y oración.

En el siguiente cuadro podemos ver como las expresiones x; 10 + x; 18 - x, así como 10 + x = 18  - x son semejantes a una oración, a través de las cuales comunicamos una idea concreta.

le tenemos que sumar a 10	10+X
LENGUAJE COMÚN	EXPRESIÓN
Queremos saber qué número	X
y restar a 18	18-X
para obtener la misma cantidad	10+X=18-X

Raicez:

La raíz (x₁) de una función lineal es el valor de x que se corresponde con el valor de ordenada cero, es decir, (x₁, 0).

Para que un número sea raíz de una función debe cumplirse que:

ƒ: R → R tak que ƒ(x) = mx + b, con m ≠ 0 si y sólo si ƒ(x₁) = 0

Estudiemos un ejemplo de análisis de función lineal para aclarar los conceptos antes mencionados.

Ejemplo:

Ejercicio: Calcular la raíz, indicar la ordenada al origen y pendiente de la recta: y = 3x+6. Graficar.

Utilizamos la ecuación de la recta para determinar cuál es la ordenada al origen y la pendiente.

m = 3

b = 6

Cálculo de la raíz

y = 3x+6

Reemplazamos a la y, por 0:

0 = 3x + 6

Despejamos la x:

-6 = 3x

-6/3 = x

x = -2 - Raíz de la función

Con estos datos podemos graficar. Ubicamos el punto de la raíz, el de la ordenada al origen y luego trazamos una recta que pase por estos dos puntos.

Características de la pendiente:

La pendiente está relacionada con el coeficiente angular, ya que m = tg α. La misma nos indica la inclinación de la recta con respecto al eje x.

Si la pendiente es positiva, la función es creciente:

Si la pendiente es negativa, la función es decreciente:

Cuando la pendiente es cero, la función es constante.

Nombre del.autor: Alan perez coronel N.L:32